Computer Science Technical & Coding Interview: April 2020

109. Convert Sorted List to Binary Search Tree

Given a singly linked list where elements are sorted in ascending order, convert it to a height balanced BST.

For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.

Example:

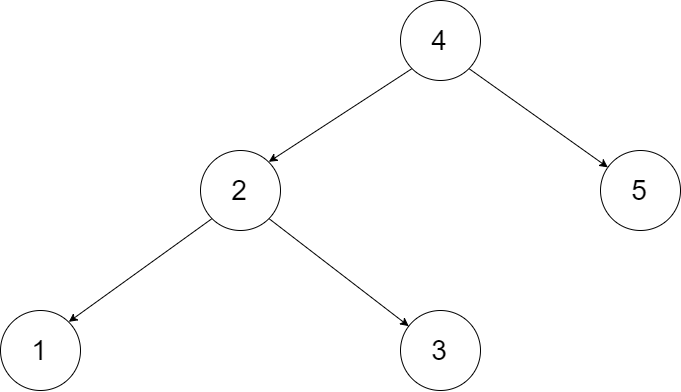
Given the sorted linked list: [-10,-3,0,5,9],

One possible answer is: [0,-3,9,-10,null,5], which represents the following height balanced BST:

      0
     / \
   -3   9
   /   /
 -10  5

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* sortedListToBST(ListNode* head) {
        ListNode *slow = head;
        ListNode *fast = head;
        ListNode *prev = NULL;
        if (head == NULL) {
            return NULL;
        }

        while (fast != NULL && fast -> next != NULL) {
            prev = slow;
            slow = slow -> next;
            fast = fast -> next -> next;
        }
        ListNode *secondHalf = slow -> next;
        slow -> next = NULL;
        TreeNode *root = new TreeNode(slow -> val);
        if (prev != NULL) {
            prev -> next = NULL;
        } else {
            return root;
        }
        root -> left = sortedListToBST(head);
        root -> right = sortedListToBST(secondHalf);
        return root;
    }
};

class Solution {
public:
    
    
    TreeNode* listToBST(ListNode *head){
        
        if(head==NULL)
            return NULL;
        TreeNode *root;
        ListNode *slow, *fast, *prev_slow, *temp;
        slow = head;
        fast = head;
        prev_slow = head;
        temp = head;
        
        while(fast!=NULL&&fast->next!=NULL){
            fast = fast->next->next;
            prev_slow = slow;
            slow = slow->next;
        }
        
        
        
        
        if(slow==fast){   
            root = new TreeNode(head->val);
            return root;
        }
        else if(fast==NULL){
            root = new TreeNode(slow->val);
            prev_slow->next = NULL;
            root->left = listToBST(head);
            root->right = listToBST(slow->next);
        }else{
             root = new TreeNode(slow->val);
            slow = slow->next;
            prev_slow->next = NULL;
            root->left = listToBST(head);
            root->right = listToBST(slow);
        }
        return root;
        
        
    }
    
    TreeNode* sortedListToBST(ListNode* head) {
  
        return listToBST(head);
        
    }
};

426. Convert Binary Search Tree to Sorted Doubly Linked List

Convert a Binary Search Tree to a sorted Circular Doubly-Linked List in place.

You can think of the left and right pointers as synonymous to the predecessor and successor pointers in a doubly-linked list. For a circular doubly linked list, the predecessor of the first element is the last element, and the successor of the last element is the first element.

We want to do the transformation in place. After the transformation, the left pointer of the tree node should point to its predecessor, and the right pointer should point to its successor. You should return the pointer to the smallest element of the linked list.

Example 1:

Input: root = [4,2,5,1,3]


Output: [1,2,3,4,5]

Explanation: The figure below shows the transformed BST. The solid line indicates the successor relationship, while the dashed line means the predecessor relationship.

Example 2:

Input: root = [2,1,3]
Output: [1,2,3]

Example 3:

Input: root = []
Output: []
Explanation: Input is an empty tree. Output is also an empty Linked List.

Example 4:

Input: root = [1]
Output: [1]

Constraints:

-1000 <= Node.val <= 1000
Node.left.val < Node.val < Node.right.val
All values of Node.val are unique.
0 <= Number of Nodes <= 2000

// Definition for a Node.

class Node {

public:

int val;

Node* left;

Node* right;

Node() {}

Node(int _val) {

val = _val;

left = NULL;

right = NULL;

}

Node(int _val, Node* _left, Node* _right) {

val = _val;

left = _left;

right = _right;

}

};

class Solution {

public:

Node* treeToDoublyList(Node* root) {

if (root == NULL) {

return root;

}

Node *head = NULL, *tail = NULL;

helper(root, head, tail);

head -> left = tail;

tail -> right = head;

return head;

}

void helper(Node* root, Node* &head, Node* &tail) {

if (root == NULL) {

return;

}

helper(root -> left, head, tail);

if (head == NULL) {

head = root;

} else {

tail -> right = root;

root -> left = tail;

}

tail = root;

helper(root -> right, head, tail);

}

};

======= Iterative ====

void iterative_helper(TreeNode* root, TreeNode *&head, TreeNode *&tail) {

if (root == NULL) {

return;

}

stack<TreeNode*> st;

TreeNode* node = root;

while(node != NULL || !st.empty()) {

while (node != NULL) {

st.push(node);

node = node -> left;

}

TreeNode* poped_node = st.top(); st.pop();

if (head == NULL) {

head = poped_node;

tail = poped_node;

} else {

tail -> right = poped_node;

poped_node -> left = tail;

tail = poped_node;

}

node = poped_node -> right;

}

head -> left = tail;

tail -> right = head;

}

========================== iterative approach O(log n) space ====== https://www.cnblogs.com/grandyang/p/9615871.html

class Solution {
public:
    Node* treeToDoublyList(Node* root) {
        if (!root) return NULL;
        Node *head = NULL, *pre = NULL;
        stack<Node*> st;
        while (root || !st.empty()) {
            while (root) {
                st.push(root);
                root = root->left;
            }
            root = st.top(); st.pop();
            if (!head) head = root;
            if (pre) {
                pre->right = root;
                root->left = pre;
            }
            pre = root;
            root = root->right;
        }
        head->left = pre;
        pre->right = head;
        return head;
    }
};