Given a binary tree, return the vertical order traversal of its nodes values.
For each node at position
(X, Y), its left and right children respectively will be at positions (X-1, Y-1) and (X+1, Y-1).
Running a vertical line from
X = -infinity to X = +infinity, whenever the vertical line touches some nodes, we report the values of the nodes in order from top to bottom (decreasing Y coordinates).
If two nodes have the same position, then the value of the node that is reported first is the value that is smaller.
Return an list of non-empty reports in order of
X coordinate. Every report will have a list of values of nodes.
Example 1:
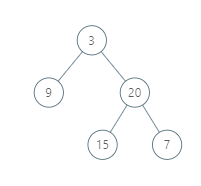
Input: [3,9,20,null,null,15,7] Output: [[9],[3,15],[20],[7]] Explanation: Without loss of generality, we can assume the root node is at position (0, 0): Then, the node with value 9 occurs at position (-1, -1); The nodes with values 3 and 15 occur at positions (0, 0) and (0, -2); The node with value 20 occurs at position (1, -1); The node with value 7 occurs at position (2, -2).
Example 2:
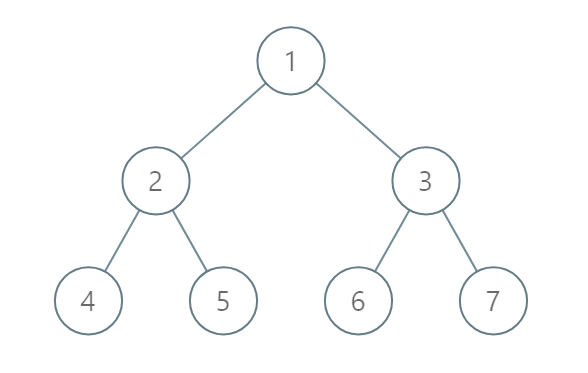
Input: [1,2,3,4,5,6,7] Output: [[4],[2],[1,5,6],[3],[7]] Explanation: The node with value 5 and the node with value 6 have the same position according to the given scheme. However, in the report "[1,5,6]", the node value of 5 comes first since 5 is smaller than 6.
Note:
- The tree will have between 1 and
1000nodes. - Each node's value will be between
0and1000.
===================== Pre order traversal is not the right approach here =======
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<vector<int>> verticalTraversal(TreeNode* root) {
if (root == NULL) {
return vector<vector<int>>();
}
vector<vector<int>> ans;
map<int, vector<int>> mp;
helper(root, 0, mp);
generate(mp, ans);
return ans;
}
void helper(TreeNode* root, int location, map<int, vector<int>>& mp) {
if (root == NULL) {
return;
}
mp[location].push_back(root -> val);
helper(root -> left, location - 1, mp);
helper(root -> right, location + 1, mp);
return;
}
void generate(map<int, vector<int>>& mp, vector<vector<int>>& ans) {
map<int, vector<int>>::iterator it;
for (it = mp.begin(); it != mp.end(); it++) {
ans.push_back(it -> second);
}
return;
}
};
========== . Queue is not working as well =====
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<vector<int>> verticalTraversal(TreeNode* root) {
if (root == NULL) {
return vector<vector<int>>();
}
vector<vector<int>> ans;
map<int, vector<int>> mp;
helper(root, 0, mp);
generate(mp, ans);
return ans;
}
void helper(TreeNode* root, int location, map<int, vector<int>>& mp) {
if (root == NULL) {
return;
}
queue<pair<int, TreeNode*>> q;
q.push(make_pair(0, root));
while (!q.empty()) {
pair<int, TreeNode*> node = q.front(); q.pop();
mp[node.first].push_back(node.second -> val);
if (node.second -> left) {
q.push(make_pair(node.first - 1, node.second -> left));
}
if (node.second -> right) {
q.push(make_pair(node.first + 1, node.second -> right));
}
}
}
void generate(map<int, vector<int>>& mp, vector<vector<int>>& ans) {
map<int, vector<int>>::iterator it;
for (it = mp.begin(); it != mp.end(); it++) {
ans.push_back(it -> second);
}
return;
}
};
================== Right one ============
class Solution
{
public:
vector<vector<int>> verticalTraversal(TreeNode* root)
{
vector<vector<int>> result;
map<int,map<int,vector<int>>> total;
deque<TreeNode*> q;
deque<int> p;
deque<int> h;
q.push_back(root);
p.push_back(0);
h.push_back(0);
while(q.size()>0)
{
TreeNode* c=q.front();
int x=p.front();
int y=h.front();
q.pop_front();
p.pop_front();
h.pop_front();
total[x][y].push_back(c->val);
if(c->left!=NULL)
{
q.push_back(c->left);
p.push_back(x-1);
h.push_back(y+1);
}
if(c->right!=NULL)
{
q.push_back(c->right);
p.push_back(x+1);
h.push_back(y+1);
}
}
for(map<int,map<int,vector<int>>>::iterator it1=total.begin();it1!=total.end();it1++)
{
vector<int> temp;
for(map<int,vector<int>>::iterator it2=it1->second.begin();it2!=it1->second.end();it2++)
{
sort(it2->second.begin(),it2->second.end());
for(int i=0;i<it2->second.size();i++)
{
temp.push_back(it2->second[i]);
}
}
result.push_back(temp);
}
return result;
}
};