986. Interval List Intersections

Given two lists of closed intervals, each list of intervals is pairwise disjoint and in sorted order.

Return the intersection of these two interval lists.

(Formally, a closed interval [a, b] (with a <= b) denotes the set of real numbers x with a <= x <= b.  The intersection of two closed intervals is a set of real numbers that is either empty, or can be represented as a closed interval.  For example, the intersection of [1, 3] and [2, 4] is [2, 3].)

Example 1:

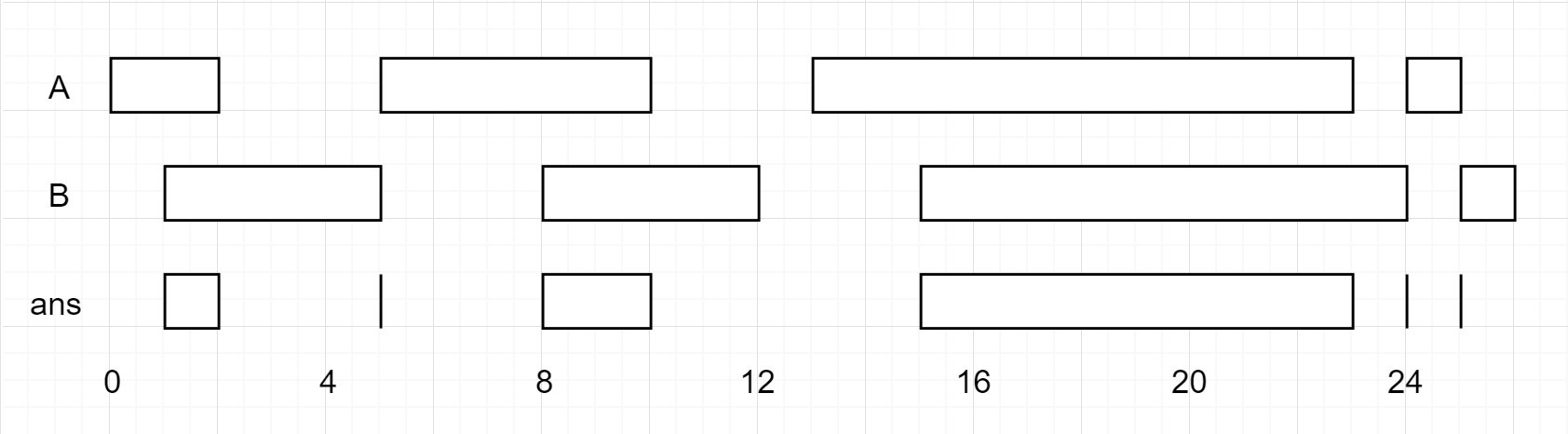
Input: A = [[0,2],[5,10],[13,23],[24,25]], B = [[1,5],[8,12],[15,24],[25,26]]
Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]
Reminder: The inputs and the desired output are lists of Interval objects, and not arrays or lists.

Note:

1. 0 <= A.length < 1000
2. 0 <= B.length < 1000
3. 0 <= A[i].start, A[i].end, B[i].start, B[i].end < 10^9

class Solution {
public:
   
    vector<int> intersect(vector<int>& A, vector<int>& B) {
        vector<int> ans;
        if (B[0] > A[1] || A[0] > B[1]) {
            return ans;
        }
        ans = {max(A[0], B[0]), min(A[1], B[1])};
        return ans;
    }
   
    vector<vector<int>> intervalIntersection(vector<vector<int>>& A, vector<vector<int>>& B) {
        vector<vector<int>> ans;
        if (A.size() == 0 || B.size() == 0) {
            return ans;
        }
       
        int size_a = A.size();
        int size_b = B.size();       
        int first = 0, second = 0;
       
        while (first < size_a && second < size_b) {
            vector<int> sol = intersect(A[first], B[second]);
            if (sol.size() > 0) {
                ans.push_back(sol);
            }
            if (A[first][1] > B[second][1]) {
                second++;
            } else if (A[first][1] < B[second][1]) {
                first++;
            } else {
                first++;
                second++;
            }
        } 
        return ans;
    }
};