Is Graph Bipartite?

 There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node uis adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:

• There are no self-edges (graph[u] does not contain u).
• There are no parallel edges (graph[u] does not contain duplicate values).
• If v is in graph[u], then u is in graph[v] (the graph is undirected).
• The graph may not be connected, meaning there may be two nodes u and v such that there is no path between them.

A graph is bipartite if the nodes can be partitioned into two independent sets A and Bsuch that every edge in the graph connects a node in set A and a node in set B.

Return true if and only if it is bipartite.

 

Example 1:

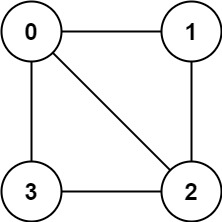
Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
Output: false
Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.

Example 2:

Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.

 

Constraints:

• graph.length == n
• 1 <= n <= 100
• 0 <= graph[u].length < n
• 0 <= graph[u][i] <= n - 1
• graph[u] does not contain u.
• All the values of graph[u] are unique.
• If graph[u] contains v, then graph[v] contains u.

class Solution {

public:

    bool isBipartite(vector<vector<int>>& graph) {

        set<int> set_a;

        set<int> set_b;

        bool ans = true;

        vector<bool> visited(graph.size(), false);

       for (int i = 0; i < graph.size(); i++) {

           if (!visited[i]) {

                dfs(graph, i, visited, set_a, set_b, ans);

                if (!ans) {

                    return false;

                }

           }

       }

        return ans;

    }

    

    void dfs(vector<vector<int>>& graph, int node, vector<bool>& visited,

            set<int>& set_a, set<int>& set_b, bool& ans) {

        if (visited[node] == true || !ans) {

            return;

        }

        visited[node] = true;

        for (auto neighbor : graph[node]) {

            if (set_a.count(node) != 0) {

                if (set_a.count(neighbor) != 0) {

                    ans = false;

                    return;

                }

                set_b.insert(neighbor);

            } else if (set_b.count(node) != 0) {

                if (set_b.count(neighbor) != 0) {

                    ans = false;

                    return;

                }

                set_a.insert(neighbor);

            } else {

                set_a.insert(node);

                if (set_a.count(neighbor) != 0) {

                    ans = false;

                    return;

                }

                set_b.insert(neighbor);

            }

            dfs(graph, neighbor, visited, set_a, set_b, ans);

        }

    }

};

================ Space optimized =========

https://zxi.mytechroad.com/blog/graph/leetcode-785-is-graph-bipartite/

Solution: Graph Coloring

For each node

• If has not been colored, color it to RED(1).
• Color its neighbors with a different color RED(1) to BLUE(-1) or BLUE(-1) to RED(-1).

If we can finish the coloring then the graph is bipartite. All red nodes on the left no connections between them and all blues nodes on the right, again no connections between them. red and blue nodes are neighbors.

Time complexity: O(V+E)

Space complexity: O(V)

// Author: Huahua

// Running time: 12 ms

class Solution {

public:

  bool isBipartite(vector<vector<int>>& graph) {

    const int n = graph.size();

    vector<int> colors(n);

    for (int i = 0; i < n; ++i)

      if (!colors[i] && !coloring(graph, colors, 1, i))

        return false;

    return true;

  }

private:

  bool coloring(const vector<vector<int>>& graph, vector<int>& colors, int color, int node) {    

    if (colors[node]) return colors[node] == color;

    colors[node] = color;

    for (int nxt : graph[node])

      if (!coloring(graph, colors, -color, nxt)) return false;

    return true;

  }

};

============= 2nd time ========

    bool isBipartite(vector<vector<int>>& graph) {

        int size = graph.size();

        if (size == 0) {

            return false;

        }

        vector<int> colors(size, -1);

        vector<bool> visited(size, false);

        bool ans = true;

        for (int i = 0; i < visited.size(); i++) {

            bool node = visited[i];

            if (!node) {

                ans = helper(i, graph, colors, 1, visited);

                if (!ans) {

                    return false;

                }

            }

        }

        return true;

    }

    

    bool helper(int start, vector<vector<int>>& graph, vector<int>& colors, int color, vector<bool>& visited) {

        if (colors[start] == color) {

            return false;

        }

        int new_color = (color + 1) % 2;

        colors[start] = new_color;

        if (visited[start]) {

            return true;

        }

        visited[start] = true;

        for (auto neighbor : graph[start]) {

            if (!helper(neighbor, graph, colors, new_color, visited)) {

                return false;

            }

        }

        return true;

    }

    ============================ Iterative one ==========

class Solution {

public:

    bool isBipartite(vector<vector<int>>& graph) {

        int n = graph.size();

        vector<int> color(n, -1);

        for (int start = 0; start < n; ++start) {

            if (color[start] == -1) {

                stack<int> stk;

                stk.push(start);

                color[start] = 0;

                while (!stk.empty()) {

                    int node = stk.top();

                    stk.pop();

                    for (int neigh : graph[node]) {

                        if (color[neigh] == -1) {

                            stk.push(neigh);

                            color[neigh] = color[node] ^ 1;

                        } else if (color[neigh] == color[node]) {

                            return false;

                        }

                    }

                }

            }

        }

        return true;

    }

};