333. Largest BST Subtree

 Given the root of a binary tree, find the largest subtree, which is also a Binary Search Tree (BST), where the largest means subtree has the largest number of nodes.

A Binary Search Tree (BST) is a tree in which all the nodes follow the below-mentioned properties:

• The left subtree values are less than the value of their parent (root) node's value.
• The right subtree values are greater than the value of their parent (root) node's value.

Note: A subtree must include all of its descendants.

Follow up: Can you figure out ways to solve it with O(n) time complexity?

 

Example 1:

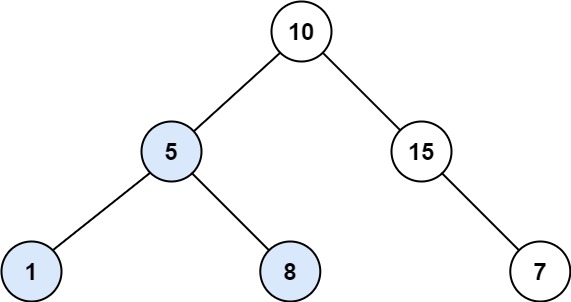
Input: root = [10,5,15,1,8,null,7]
Output: 3
Explanation: The Largest BST Subtree in this case is the highlighted one. The return value is the subtree's size, which is 3.

/**

 * Definition for a binary tree node.

 * struct TreeNode {

 *     int val;

 *     TreeNode *left;

 *     TreeNode *right;

 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}

 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}

 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}

 * };

 */

class Solution {

public:

    int largestBSTSubtree(TreeNode* root) {

        int ans = 0;

        int min_left = INT_MAX, max_right = INT_MIN;

        helper(root, ans, min_left, max_right);

        return ans;

    }

    

    pair<bool, int> helper(TreeNode* root, int& ans, int& min_left, int& max_right) {

        if (root == NULL) {

            return {true, 0};

        }

        int left_min = INT_MAX, left_max = INT_MIN,

            right_min = INT_MAX, right_max = INT_MIN;

        pair<bool, int> left = helper(root -> left, ans, left_min, left_max);

        pair<bool, int> right = helper(root -> right, ans, right_min, right_max);

        min_left = min(root -> val, left_min);

        max_right = max(root -> val, right_max);

        

        if (left.first && right.first) {

            if (root -> val > left_max && root -> val < right_min) {

                ans = max(ans, left.second + right.second + 1);

                return {true, left.second + right.second + 1};

            }

        } 

        ans = max(ans, 1);

        return {false, 0};

    }

};

======= Another one ====

class Solution { public: int largestBSTSubtree(TreeNode* root) { int count = 0, min = INT_MIN, max = INT_MAX; helper(root, count, min, max); return count; } bool helper(TreeNode* root, int& count, int& minimum, int& maximum){ if(root == nullptr) return true; int leftCount = 0, lmin = INT_MIN, lmax = INT_MAX; int rightCount = 0, rmin = INT_MIN, rmax = INT_MAX; //Null checking bool left = helper(root->left, leftCount, lmin, lmax); bool right = helper(root->right, rightCount, rmin, rmax); if(left && right) { if((root->left == nullptr || root->val > lmax )&& (root->right == nullptr || root->val < rmin)){ minimum = root->left ? lmin : root->val; maximum = root->right ? rmax : root->val; count = leftCount + rightCount + 1; return true; } } count = max(leftCount, rightCount); return false; } };