All Nodes Distance K in Binary Tree

We are given a binary tree (with root node root), a target node, and an integer value K.

Return a list of the values of all nodes that have a distance K from the target node.  The answer can be returned in any order.

Example 1:

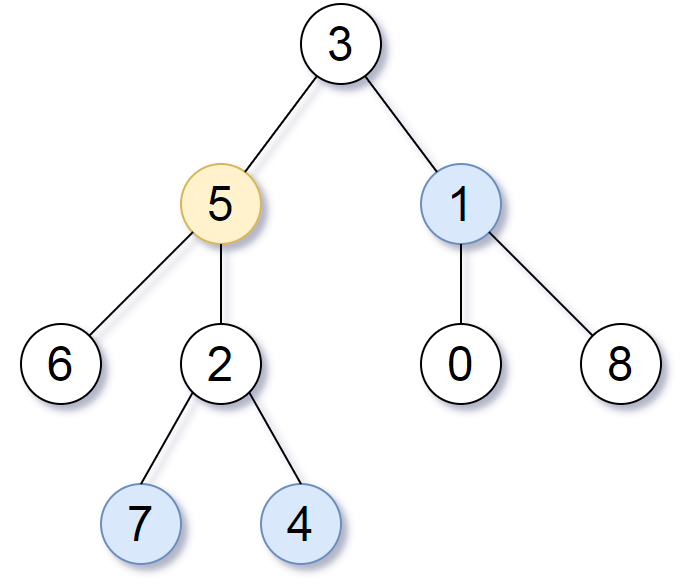
Input: root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, K = 2

Output: [7,4,1]

Explanation: 
The nodes that are a distance 2 from the target node (with value 5)
have values 7, 4, and 1.



Note that the inputs "root" and "target" are actually TreeNodes.
The descriptions of the inputs above are just serializations of these objects.

Note:

1. The given tree is non-empty.
2. Each node in the tree has unique values 0 <= node.val <= 500.
3. The target node is a node in the tree.
4. 0 <= K <= 1000.

Approach 1: Annotate Parent

Intuition

If we know the parent of every node x, we know all nodes that are distance 1 from x. We can then perform a breadth first search from the target node to find the answer.

Algorithm

We first do a depth first search where we annotate every node with information about it's parent.

After, we do a breadth first search to find all nodes a distance K from the target.

Complexity Analysis

• Time Complexity: $O(N)$, where $N$ is the number of nodes in the given tree.
• Space Complexity: $O(N)$. 
  

---

Approach 2: Percolate Distance

Intuition

From root, say the target node is at depth 3 in the left branch. It means that any nodes that are distance K - 3 in the right branch should be added to the answer.

Algorithm

Traverse every node with a depth first search dfs. We'll add all nodes x to the answer such that node is the node on the path from x to target that is closest to the root.

To help us, dfs(node) will return the distance from node to the target. Then, there are 4 cases:

• If node == target, then we should add nodes that are distance K in the subtree rooted at target.
• If target is in the left branch of node, say at distance L+1, then we should look for nodes that are distance K - L - 1 in the right branch.
• If target is in the right branch of node, the algorithm proceeds similarly.
• If target isn't in either branch of node, then we stop.

In the above algorithm, we make use of the auxillary function subtree_add(node, dist)which adds the nodes in the subtree rooted at node that are distance K - dist from the given node.

Complexity Analysis

• Time Complexity: $O(N)$, where $N$ is the number of nodes in the given tree.
• Space Complexity: $O(N)$.