/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<int> distanceK(TreeNode* root, TreeNode* target, int K) {
vector<int> ans;
if (root == NULL || target == NULL) {
return ans;
}
if (K == 0) {
return {target->val};
}
// Prepare parentMap
unordered_map<TreeNode*, TreeNode*> mp;
PrepareParent(root, NULL, mp);
// BFS
return BFS(target, mp, K);
}
void PrepareParent(TreeNode* root, TreeNode *parent, unordered_map<TreeNode*, TreeNode*>& mp) {
if (root == NULL) {
return;
}
mp[root] = parent;
PrepareParent(root -> left, root, mp);
PrepareParent(root -> right, root, mp);
}
void checkNode(TreeNode *node, queue<TreeNode *>& q, unordered_set<TreeNode *>& visited, vector<int>& ans, int level, int k) {
if (node != NULL && visited.count(node) == 0) {
visited.insert(node);
if (level == k - 1) {
ans.push_back(node -> val);
} else {
q.push(node);
}
}
}
vector<int> BFS(TreeNode* node, unordered_map<TreeNode*, TreeNode*>& mp, int k) {
vector<int> ans;
unordered_set<TreeNode *> visited;
queue<TreeNode *> q;
q.push(node);
visited.insert(node);
int level = 0;
while (!q.empty()) {
int size = q.size();
for (int i = 0; i < size; i++) {
TreeNode *node = q.front(); q.pop();
// All neighbors (both child + parent)
TreeNode * left = node -> left;
checkNode(left, q, visited, ans, level, k);
TreeNode * right = node -> right;
checkNode(right, q, visited, ans, level, k);
TreeNode * parent = mp[node];
checkNode(parent, q, visited, ans, level, k);
}
level++;
}
return ans;
}
// DFS one is shorter too
/*
class Solution {
public:
vector<int> ans;
map<TreeNode*, TreeNode*> parent; // son=>parent
set<TreeNode*> visit; //record visied node
void findParent(TreeNode* node){
if(!node ) return;
if( node->left ){
parent[node->left] = node;
findParent(node->left);
}
if( node->right){
parent[node->right] = node;
findParent(node->right);
}
}
vector<int> distanceK(TreeNode* root, TreeNode* target, int K) {
if( !root ) return {};
findParent(root);
dfs(target, K );
return ans;
}
void dfs( TreeNode* node, int K){
if( visit.find(node) != visit.end() )
return;
visit.insert(node);
if( K == 0 ){
ans.push_back(node->val);
return;
}
if( node->left ){
dfs(node->left, K-1);
}
if( node->right){
dfs(node->right, K-1);
}
TreeNode* p = parent[node];
if( p )
dfs(p, K-1);
}
};
*/
};
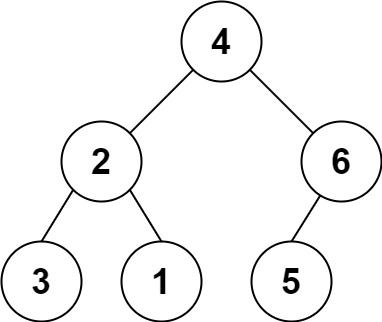
Note that the inputs "root" and "target" are actually TreeNodes. The descriptions of the inputs above are just serializations of these objects.