1428. Leftmost Column with at Least a One

 (This problem is an interactive problem.)

A row-sorted binary matrix means that all elements are 0 or 1 and each row of the matrix is sorted in non-decreasing order.

Given a row-sorted binary matrix binaryMatrix, return the index (0-indexed) of the leftmost column with a 1 in it. If such an index does not exist, return -1.

You can't access the Binary Matrix directly. You may only access the matrix using a BinaryMatrix interface:

• BinaryMatrix.get(row, col) returns the element of the matrix at index (row, col) (0-indexed).
• BinaryMatrix.dimensions() returns the dimensions of the matrix as a list of 2 elements [rows, cols], which means the matrix is rows x cols.

Submissions making more than 1000 calls to BinaryMatrix.get will be judged Wrong Answer. Also, any solutions that attempt to circumvent the judge will result in disqualification.

For custom testing purposes, the input will be the entire binary matrix mat. You will not have access to the binary matrix directly.

 

Example 1:

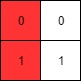
Input: mat = [[0,0],[1,1]]
Output: 0

Example 2:

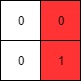
Input: mat = [[0,0],[0,1]]
Output: 1

Example 3:

Input: mat = [[0,0],[0,0]]
Output: -1

Example 4:

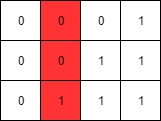
Input: mat = [[0,0,0,1],[0,0,1,1],[0,1,1,1]]
Output: 1

 

Constraints:

• rows == mat.length
• cols == mat[i].length
• 1 <= rows, cols <= 100
• mat[i][j] is either 0 or 1.
• mat[i] is sorted in non-decreasing order.

/**

 * // This is the BinaryMatrix's API interface.

 * // You should not implement it, or speculate about its implementation

 * class BinaryMatrix {

 *   public:

 *     int get(int row, int col);

 *     vector<int> dimensions();

 * };

 */

int binary_search(BinaryMatrix &binaryMatrix, int row, int col) {

    int st = 0;

    int end = col;

    while (st <= end) {

        int mid = st + (end - st)/2;

        if (binaryMatrix.get(row, mid) == 1) {

            end = mid - 1;

        } else {

            st = mid + 1;

        }

    }

    if (end == col) {

        return end;

    }

    return end + 1;

}

class Solution {

public:

    int leftMostColumnWithOne(BinaryMatrix &binaryMatrix) {

        vector<int> dims = binaryMatrix.dimensions();

        int rows = dims[0];

        int cols = dims[1];

        if (rows == 0 || cols == 0) {

            return 0;

        }

        

        int row = 0, col = cols - 1;

        int flag = -1;

        while (row < rows) {

            int col_idx = binary_search(binaryMatrix, row, col);

            if (col_idx == 0) {

                return 0;

            }

            // Distinguish between the last cols having value 1 or not.

            if (binaryMatrix.get(row, col_idx) == 1) {

                flag = 1;

            }

            col = min(col, col_idx);

            row++;

        }

        

        return (col == cols - 1 ? flag : col);

    }

    

};

========== Cleaner one (except binary search mid logic)========

int leftMostColumnWithOne(BinaryMatrix &binaryMatrix) { auto vec = binaryMatrix.dimensions(); auto rows = vec[0]; auto cols = vec[1]; int min = cols + 1; for (int i = 0; i < rows; ++i) { // search over the rows int l = 0; int r = cols; while (l < r) { int mid = (l + r) / 2; // cout << mid << "\n"; if (binaryMatrix.get(i, mid) == 0) { l = mid + 1; } else { r = mid; } } if (l < cols) { min = std::min(min, l); } } if (min == cols + 1) return - 1; return min; }

=============== Best solution is ======= O(n + m) ======

public int leftMostColumnWithOne(BinaryMatrix binaryMatrix) { int rows = binaryMatrix.dimensions().get(0); int cols = binaryMatrix.dimensions().get(1); // Set pointers to the top-right corner. int currentRow = 0; int currentCol = cols - 1; // Repeat the search until it goes off the grid. while (currentRow < rows && currentCol >= 0) { if (binaryMatrix.get(currentRow, currentCol) == 0) { currentRow++; } else { currentCol--; } } // If we never left the last column, this is because it was all 0's. return (currentCol == cols - 1) ? -1 : currentCol + 1; }

======== tried ======

int leftMostColumnWithOne(BinaryMatrix &binaryMatrix) { vector<int> dims = binaryMatrix.dimensions(); int rows = dims[0], cols = dims[1]; int ans = INT_MAX; int col = cols - 1, row = 0; while (col >= 0 || row < rows) { while (col >= 0 && binaryMatrix.get(row, col) != 0) { ans = min(ans, col); col--; } if (col == -1) { return 0; } row++; if (row == rows) { break; } } return ans == INT_MAX ? -1: ans; }

================

int leftMostColumnWithOne(BinaryMatrix &binaryMatrix) { vector<int> dims = binaryMatrix.dimensions(); if (dims[0] == 0 || dims[1] == 0) { return -1; } int row_it = 0; int col_it = dims[1] - 1; int ans = INT_MAX; while (row_it < dims[0] && col_it >= 0) { if (binaryMatrix.get(row_it, col_it) == 1) { ans = col_it; col_it--; } else { row_it++; } } return (ans == INT_MAX ? -1: ans); }