669. Trim a Binary Search Tree

 Given the root of a binary search tree and the lowest and highest boundaries as low and high, trim the tree so that all its elements lies in [low, high]. Trimming the tree should not change the relative structure of the elements that will remain in the tree (i.e., any node's descendant should remain a descendant). It can be proven that there is a unique answer.

Return the root of the trimmed binary search tree. Note that the root may change depending on the given bounds.

 

Example 1:

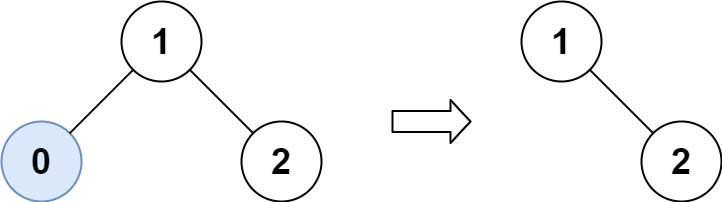
Input: root = [1,0,2], low = 1, high = 2
Output: [1,null,2]

Example 2:

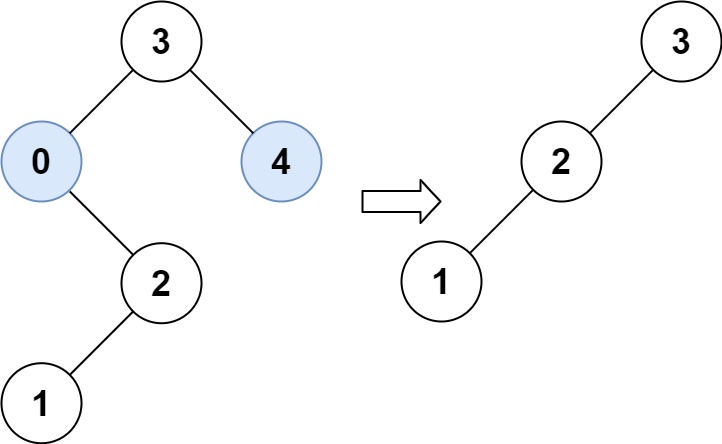
Input: root = [3,0,4,null,2,null,null,1], low = 1, high = 3
Output: [3,2,null,1]

Example 3:

Input: root = [1], low = 1, high = 2
Output: [1]

Example 4:

Input: root = [1,null,2], low = 1, high = 3
Output: [1,null,2]

Example 5:

Input: root = [1,null,2], low = 2, high = 4
Output: [2]

 

Constraints:

• The number of nodes in the tree in the range [1, 104].
• 0 <= Node.val <= 104
• The value of each node in the tree is unique.
• root is guaranteed to be a valid binary search tree.
• 0 <= low <= high <= 104

/**

 * Definition for a binary tree node.

 * struct TreeNode {

 *     int val;

 *     TreeNode *left;

 *     TreeNode *right;

 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}

 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}

 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}

 * };

 */

class Solution {

public:

    TreeNode* trimBST(TreeNode* root, int low, int high) {

        if (root == NULL) {

            return NULL;

        }

        if (root -> val > high) {

            return trimBST(root -> left, low, high);

        } else if (root -> val < low) {

            return trimBST(root -> right, low, high);

        }

        root -> left = trimBST(root -> left, low, high);

        root -> right = trimBST(root -> right, low, high);

        return root;

    }

};